6辆骑车排成一列纵队,要求甲车和乙车均不在队头或队尾,且两车间隔两辆车,问共有多少种不同的排法?
A.48
B.72
C.90
D.120
蜘蛛有8只脚,蜻蜓有6只脚和2对翅膀,蝉有6只脚和1对翅膀,现在三种昆虫共18只,共有118只脚和20对翅膀,则其中有蜻蜓多少只?( )
A.5
B.6
C.7
D.8
A.47
B.48
C.50
D.51
超市经理为某商品准备了两种促销方案,第一种是原价打7折;第二种是买二件赠一件同样商品。经计算,两种方案每件商品利润相差0.1元,若按照第一种促销方案,则100元可买该商品件数最大值是( )
A.33
B.47
C.49
D.50
甲、乙两人同时从A、B两地出发,相向而行,甲到达B地后,立即往回走,回到A地后,又立即向B地走去;乙到达A地后,立即往回走,回到B地后又立即向A地走去。如此往复,行走的速度不变,若两人第二次迎面相遇的地点距A地500米,第四次迎面相遇地点距B地700米,则A、B两地的距离是( )。
A.1350米
B.1460米
C.1120米
D.1300米
1.答案:
解析:
特殊元素优先法:6个编号:1、2、3、4、5、6,要求甲乙不在队头或队尾,则甲乙只能在2-5的位置中选择,又甲乙两车间隔两辆车,2-5中,间隔2个,只能是2、5位置上安排甲乙,另外四辆车在1、3、4、6共4个位置上进行选择,故总的排列方式=A4,4×2=48种。选择A选项。
2.答案:
解析:
假设全是6只脚的昆虫,18只共有108只脚,因此多出的118—108=10(只)脚来自于10÷(8—6)=5(只)蜘蛛。而在剩下的18—5=13(只)昆虫中,假设都是1对翅膀,同样地分析可知,有蜻蜓(20—13)÷(2一1)=7(只)。
3.答案:
解析:
和为2359,求N的最大值,那么尽量从最小数连续选起,才能满足这个要求。同时,和为2359,只有奇数×奇数才为奇数,说明N必为奇数,排除B和C。而(1+99)÷2×50=2500,D选项明显大了,所以本题答案为A选项。
4.答案:
解析: 设该商品原价为x,则第一种方案下,三件促销价格为2.1x,第二种方案下,三件促销价格2x,两种方案差价为0.1x。根据题意,两种方案每件商品的利润差为0.1元,则三件商品差价0.3元,即0.1x=0.3,解得x=3元,那么按照第一种促销方案,商品售价2.1元,100元最多可以购买该商品47件,选择B项。
5.答案:
解析:
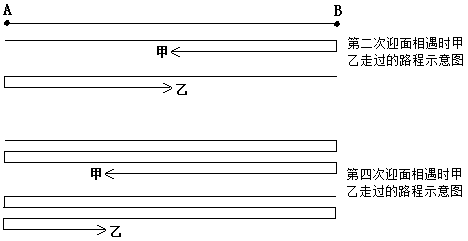
设两地距离为s。画示意图分析,第二次迎面相遇时,甲走了(2s-500)米,乙走了(s+500)米;第四次迎面相遇时,甲走了(3s+700)米,乙走了(4s-700)米。两个人走的时间一样,因此两次相遇是所走的路程的比例是一样的,则有(2s-500)/(s+500)=(3s+700)/(4s-700),解得s=1120米。故正确答案为C。